| |
|
| |
Aurthors/المؤلفون
Abstract/الملخص
Keywords/الكلمات المفتاحية
Content/أقسام الملف
1- Introduction
2- Related works
3- Surgical Robot Manipulator
4- Intelligent Control System
5- SIMULATION RESULTS
6- Developed Structure of Proposed BELBIC
7- Conclusion
8- References |
| Design of Brain Emotional Learning-Based Intelligent Controller to Solve Packet Loss Control in Surgical Robot Manipulator in Real-Time |
| |
| |
| Bashar M.(1) Joumana D.(2) |
| (1)Bashar Mousa: Ph.D. student at the Department of Automatic Control and Computers, Faculty of Mechanical and Electrical Engineering, Al-Baath University, Syria |
| (2)Joumana Al-Deab: Assistant Professor at the Department of Automatic Control and Computers, Faculty of Mechanical and Electrical Engineering, Al-Baath University, Syria |
| Bashar_mousa77@hotmail.com |
| |
|
|
Abstract
The recent development of robot technology is revolutionizing the medical field. The use of assistive robots in medical surgery is increased in worldwide. Robot-assisted surgery has the advantage of reducing surgeons' hand tremors, decreasing postoperative complications, reducing patients' pains, and increasing operation dexterity inside the patient’s bodies.
One of the most important issues in real-time remote-control systems is to provide ultra-reliable and low-latency communication between the remote controller and the control system. This is because packet loss can lead to a loss in performance control. In this research, we aim to optimize the control performance to solve the packet loss problem and overcome its adverse effects. Brain Emotional Learning-Based Intelligent Controller (BELBIC) is adopted to solve packet loss problems in real-time control. a BELBIC controller is designed, then it is utilized to control a robotic manipulator with three joints and three degrees of freedom to follow the surgeon's arm to perform the required surgical action. The simulation results of controlling the robotic manipulator using a modified BELBIC controller show a very good response of the system, where there is a small settling time, small rise time, no overshot, and overcome the adverse effects of packet loss problem. this simulation result was compared with well-tuned PID, and the result is that modified BELBIC is better than PID controller, and BELBIC can overcome the adverse effects of packet loss problems where PID can’t. |
|
|
|
| Keywords: robot technology, medical surgery, Virtual Robot arm, BELBIC, PID Controller, Packet loss. |
|
| |
|
| |
|
| 1- Introduction |
|
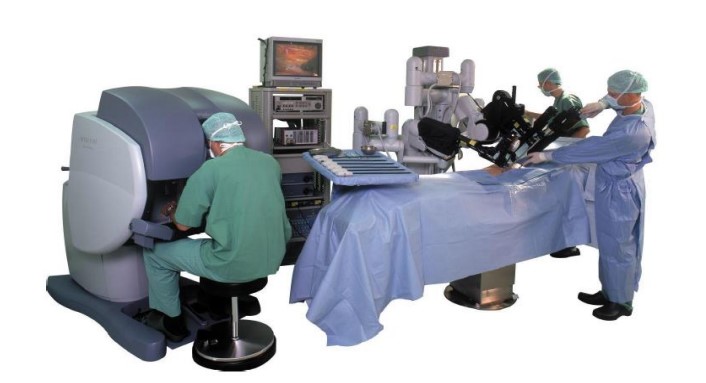
| Robot-assisted surgery have the attention of the robotics research community and the medical world in the past decade, because it improves precision, enhances dexterity, eliminates tremors, reduces complication rates, and enables novel procedures not achieved before. One of the most important implementations of robot-assisted surgery is the DAVINCI surgical system of Intuitive Surgical, which is a ‘master-slave’ type robotic system. A surgeon at a bespoke control station acts as the master controlling the end effectors of the slave multi-arm manipulator system to perform abdominal keyhole procedures on the patient. despite its capability to perform abdominal procedures, the DAVINCI system is too bulky and lacks the precision and dexterity required for delicate applications that require higher accuracy. Therefore, researchers are actively developing and implementing novel robotic systems to accommodate more demanding surgical procedures[1-3]. Figure 1 shows the DAVINCI Surgical robot System. |
|
| |
|
 |
|
| Figure 1. Intuitive Surgical DAVINCI Surgical System |
|
| |
|
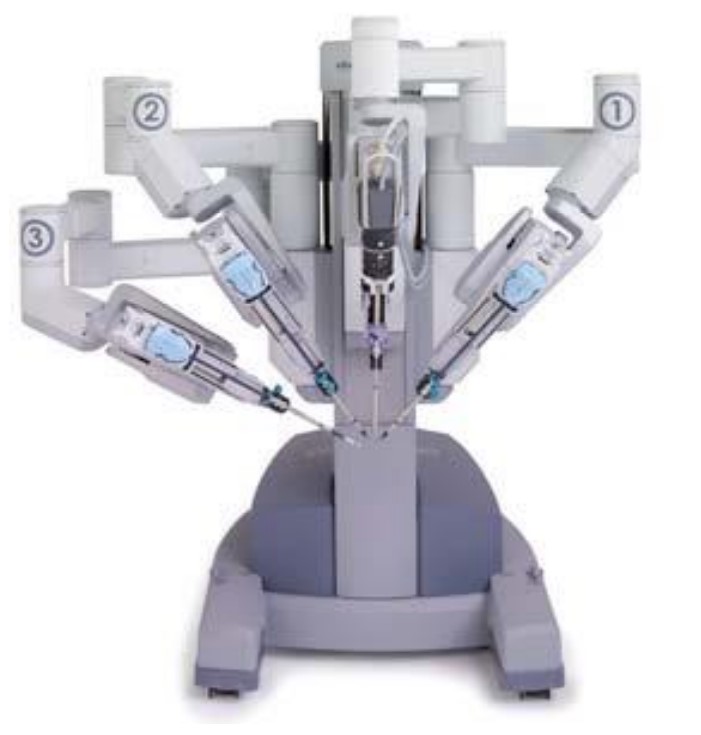
| Robot-assisted surgery has many challenges, like nonlinear manipulation, high-precision dexterous operation, insertion depth perception, and contact force feedback. Researchers started to investigate some of these concerns by developing robotic assistants, but they can't find a comprehensive robotic system that is capable of assisting general surgical procedures for the eyes, and heart and addressing existing surgical challenges. Besides, there are also many interesting robotics-related theoretical problems to be investigated under the light of surgery, e.g., multi-arm manipulation, robot performance evaluation, high-precision robot design, force sensing implementation, etc.[4-6]. Figure 2 shows the robotic manipulators in medical industries Robot manipulators are set. |
|
| |
|
 |
|
| Figure 2. The Robotic Manipulator in Medical Industries. |
|
| |
|
Robot manipulators are a set of links that are connected by joints, they are multi-input and multi-output (MIMO), nonlinear, time-variant, uncertain dynamic systems and are developed to replace human workers in many fields such as medicine. Complexities of the tasks caused the design of machine architectures and robot manipulators with nonlinear behavior.
Surgical robot manipulators are nonlinear uncertain systems with human-like behavior therefore, control of these systems is complicated. Robot manipulators are divided into two main groups, serial links robot manipulators and parallel links robot manipulators. In serial links, robot manipulator links and joints are serially connected between the base and end-effector. The study of robot manipulators is classified into two main subjects:
• kinematics
• Dynamics
The study of kinematics is important to design controllers in practical applications. Dynamic modeling of a robot manipulator is used to illustrate the behavior of the robot manipulator (e.g., MIMO, nonlinear, uncertain parameters and …), design of nonlinear conventional controllers such as conventional Computed Torque Controller and Sliding Mode Controller, and for modeling. It is also used to explain some dynamic parameters’ effects on system behavior. According to the literature [7-8], a surgical robot manipulator is a parallel link, with four degrees of freedom, and highly nonlinear dynamic systems, and modeling and control of this system are the main challenges in this research. To control of surgical robot manipulator, three purposes are very important:
• Stability: Stability is due to the proper functioning of the system. A system is called stable if, for any bounded input signal, the system’s output will stay bounded. Therefore, the limitation of output deviation is very important for any design.
• Robust: Robust method is caused to achieve robust and stable performance in the presence of uncertainty and external disturbance. A system is robust when it would also works well under different conditions and external disturbances.
• Reliability: to control nonlinear and uncertain systems, reliability play an important role and most model-based controller are reliable.
As a result, modeling and designing a controller are the main challenges in this work. A controller (control system) is a device that senses information from the system (e.g., robot manipulator) to improve the performance of the system using actuation and computation. According to the control theory, systems are divided into two main groups: conventional control theory and soft computing control theory. Conventional control theories work based on the manipulator dynamic model. This technique is highly sensitive to the knowledge of all parameters of the nonlinear robot manipulator’s dynamic equation. Conventional control theories are divided into two main groups:
• Linear control theory
• Nonlinear control theory.
Soft computing (intelligent) control theory is free of some challenges associated with conventional control theory. This technique is worked based on intelligent science like artificial neural networks, fuzzy logic, genetic algorithms, and others.
This type of theory is used in industries and some medical systems because the design of this type of controller is simple than a nonlinear controller. |
|
| |
|
| 2. Related works |
|
In Ohri et al. (Citation2011)[9], the authors present a comparison of the conventional PID controller and sliding mode control (SMC) for robotic manipulators. Both techniques have good performance, but the SMC is insensitive to parametric variations and has good disturbance rejection. The simulation results of the study show that the performance of the SMC is better than PID under both sine and cosine trajectories.
In Getachew (Citation2018)[10], the authors proposed SMC for two degrees of freedom (2-DOF) robotic manipulator systems and presented a comparative study of PID controllers. Based on simulation results and analysis, the authors concluded that the SMC controller has superior performance and is more robust when contrasted with the PID controller for sinusoidal trajectory tracking.
In Alassar et al. (Citation2010)[11], the authors introduced a fuzzy logic controller (FLC) for manipulating a 5-DOF robotic manipulator based on the independent joint control approach. The proposed controller was developed to overcome the shortcomings of the linear PID controller. The simulation was performed using MATLAB/Simulink to compare the performance of the controller in terms of time response. The results obtained were promising as the FLC was used to control complex nonlinear dynamic systems. However, the design of the FLC highly depended upon expert knowledge or trial and error. Furthermore, it didn’t guarantee stability and robustness due to the linguistic expressions of fuzzy control.
A design of computed torque control (CTC) methodology for the PUMA-560 robot manipulator was presented in (Piltan et al., Citation2012a)[12]. Computed torque control (CTC) is a powerful nonlinear controller that is extensively utilized in robot manipulator control which calculates the required torques for all manipulator’s joints using a nonlinear feedback control law based on feedback linearization. The simulation results indicate that the CTC controller works very well when all dynamic and physical parameters are known. But still, there was a problem with uncertain dynamic system models. In most physical systems like robot manipulators, the parameters are unknown or time-variant. Consequently, the authors recommended designing a sliding mode controller (SMC) to solve this problem.
In (Piltan et al., Citation2012b)[13], a novel fuzzy sliding mode controller (FSMC) was introduced to control the bus suspension system by combining fuzzy logic with an SMC. This method eliminates the two major drawbacks of SMC; firstly by using the boundary layer instead of the signum and FLC in place of the equivalent dynamic part of SMC to eliminate the chattering and equivalent dynamic dependency problem, respectively. The authors concluded from the outcome of the simulation that FSMC has better performance for the bus suspension system and is more robust as compared to the PID controller.
In Rahmdel et al. (Citation2012)[14], the authors introduced an intelligent control approach called the FSMC with global stabilization and saturation function (boundary layer method) for the trajectory tracking control of a robot manipulator. The FSMC used in their work has to chatter in it. This chattering effect of the FSMC was eliminated by applying a saturation function instead of a signum function. The authors used several conventional methods such as PD, CTC, and SMC to evaluate and contrast the proposed control method. Finally, the results of the simulation indicate that the FSMC can guarantee robustness against continuous disturbance and has a strong ability to eliminate chattering.
A nonlinear SMC was utilized in a spread-out scope of regions such as in robotics, process control, and aerospace applications in Shaei (Citation2010)[14]. The main reason this controller was used is because of its performance. Also, it solves some main challenging issues in the systems control such as resistivity to external disturbance and uncertainty. in Kapoor & Ohri (Citation2013)[15], the authors presented an SMC with saturation and hyperbolic tangent functions instead of signum functions. Unfortunately, this approach was effective only in specific cases. When hard uncertainties are not present, some problems are attenuated at the cost of a loss of robustness. Furthermore, a nonlinear FSMC was used to reduce or compensate for the negative effect of the saturation function in the system. However, both SMC and FSMC have difficulty in handling unstructured model uncertainties, because the sliding surface gain is chosen by trial and error, which means that the SMC and FSMC must have prior knowledge of the uncertainty of the system. In contrast to other papers, this work combines the fuzzy-based tuning method with FSMC to overcome the problem of handling unstructured model uncertainties to increase the robustness of the system. In (Anh et al., Citation2018)[16], an adaptive fuzzy sliding mode controller (AFSMC) to demonstrate the stability of a robotic manipulator system using the Lyapunov stability theorem was presented. Similarly, an AFSMC was proposed by (Zhang et al., Citation2020) [17] to improve the trajectory tracking accuracy of a 3-DOF serial manipulator with parameter uncertainties. |
|
| |
|
| 3. Surgical Robot Manipulator |
|
| In this research, we will study a Robot manipulator with three joints and three degrees of freedom to follow the surgeon's arm to perform the required surgical action. this robot manipulator is shown in Figure 3. |
|
| |
|
 |
|
| Figure 3. studied Robotic Manipulator |
|
| |
|
| The basics of the dynamics of the manipulator are well known and are more specifically represented in the below derivation. For an n-DOF robot manipulator, the Euler–Lagrange equation is: |
|
 |
|
| where φ, φ•, φ•• denote the position, velocity, and acceleration of the manipulator’s joint, τ is the input control torque, M(φ) is the inertia matrix, G(φ) is gravity vector, C (φ, φ•) is centripetal matrix and τd (φ, φ•) is disturbance vector |
|
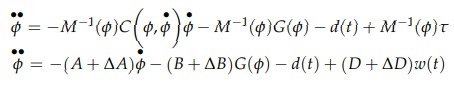 |
|
where ∆A, ∆B, ∆and D are the uncertainties present in the system; A = M−1 (φ)C (φ, φ•),
B = D = M−1 (φ),d(t) = M−1 (φ)( τd (φ, φ•) ) and w(t) = τ. For the 3DOF surgical manipulator |
|
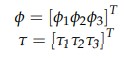 |
|
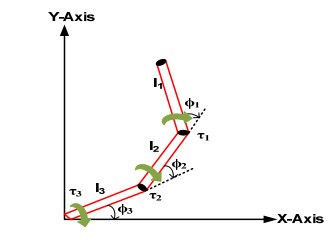
| where φ3is the angle between the base and the first link of the robotic manipulator, φ2 is the angle between the second link and first link of the robotic manipulator, and φ1is the angle between the third link and the second link of the robotic manipulator. τ1, τ2 and τ3 are the resultant torques applied on joint1, joint2, and joint3, respectively, of the surgical manipulator as shown in Figure 4. |
|
| |
|
 |
|
| Figure 4. 3DOF robotic manipulator. |
|
| |
|
| 4. Intelligent Control System |
|
In recent years, researchers around the world have considered biological intelligent systems to solve problems that cannot be solved using traditional techniques [18]. The main difference between traditional control methods and biological intelligent systems is that the latter can learn [19]. This allows for solving control problems in unknown systems or in systems in which the parameters can change due to external noise.
There are different types of intelligent systems, however, the focus here will be on the Brain’s Emotional Learning-Based Intelligent Controller (BELBIC).
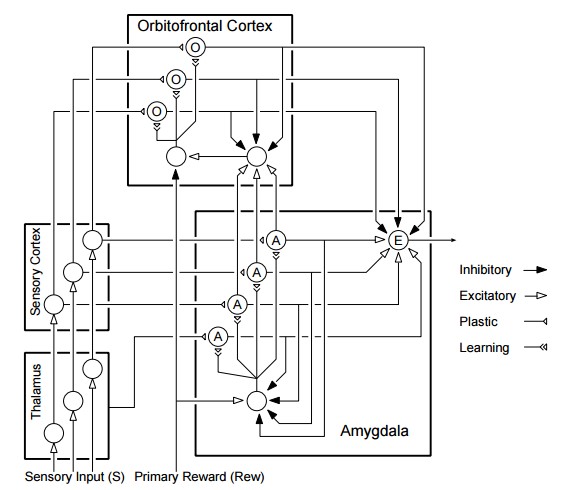
BELBIC was proposed by Moren and Balkenius in 2001. They presented a computational model based on the mammalian brain [20]. The model, as shown in Figure 5, consists of two main parts, the amygdala, and the orbitofrontal cortex. The amygdala has two inputs, one originates from the thalamus and the other originates from the cortical areas. Amygdala is where the stimulus and its emotional consequences are associated [19]. The orbitofrontal cortex has two inputs too, one originates from the cortical areas and the other originates from the amygdala. In addition, the orbitofrontal cortex is known to inhibit areas it is connected to. More specifically, the orbitofrontal cortex controls the extinction of learning in the amygdala [19] [20] [21]. |
|
| |
|
 |
|
| Figure 5: Graphical description of the brain emotional learning model [22] |
|
| |
|
| Moren and Balkenius’s computational model was modified by Lucas, who used a feedback mechanism [18]. The resultant controller, shown in Figure 5, is called Brain Emotional Learning-Based Intelligent Controller (BELBIC). BELBIC is based on sensory inputs (SI) and emotional signals (REW) [18]. There is a connection weight “V” For each “A” node. Each node gives an output that is determined by multiplying each input by the weight V, as shown in equation (4). |
|
 |
|
| Each weight Vi is adjusted proportionally using the difference between the reinforcement signal (REW) and the activation of the A nodes, as shown in equation (5). α in equation (5) is the learning rate in the amygdala, and is used to adjust the learning speed. |
|
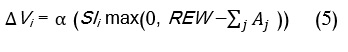 |
|
The adjusting rule for weights V is monotonic, i.e., the weights V can never decrease. When the amygdala has learned the emotional reaction, the reaction would be saved and cannot decrease. If the emotional reaction is not suitable, the orbitofrontal part will inhibit it in this case.
The second input to the amygdala part is Ath and is calculated as the maximum overall stimuli, SI, as shown in equation (6). |
|
 |
|
| The orbitofrontal learning rule is similar to that of the amygdala but with one difference. The difference is that the orbitofrontal connection weight can both increase and decrease as needed to track the required inhibition, however, the amygdala orbitofrontal connection weight can only increase. Each node O gives an output that is determined by multiplying the input signal by the weight W, as shown in equation (7). |
|
 |
|
| The learning rule in the orbitofrontal cortex is shown in equation (8). β in equation (8) is the learning rate in the orbitofrontal cortex. |
|
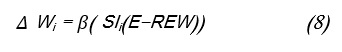 |
|
| The outputs from the A nodes are simply added together then, the inhibitory outputs from the O nodes are subtracted to get the value of node E, which is the output of the whole model. The A nodes give outputs proportionally to their contribution in predicting the reward REW, while the O nodes inhibit the output of E as necessary, as shown in equation (9) [20]. |
|
 |
|
In general, when BELBIC is used in a certain application, one should define SI and REW for that application, as REW and SI values can be chosen based on the control objectives [23]. Generally, there are two approaches, direct and indirect, to apply the brain emotional learning model to control systems. In the indirect approach, the model is used for tuning the parameters of the controller. However, in the direct approach, the model is used as a controller block [18] [19] [23] [24]. In this research, the direct approach is adopted.
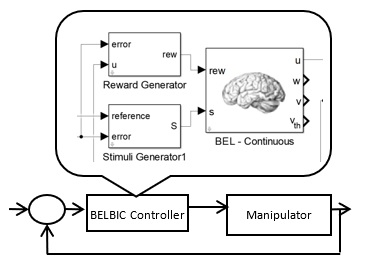
In this study, a Brain Emotional Learning-Based Intelligent Controller is designed. this BELBIC is responsible for movement control. Fig. 6 demonstrates the proposed control scheme that was built in Matlab. |
|
| |
|
 |
|
| Fig. 6 The proposed control scheme that was built in Matlab. |
|
| |
|
| 5. SIMULATION RESULTS: |
|
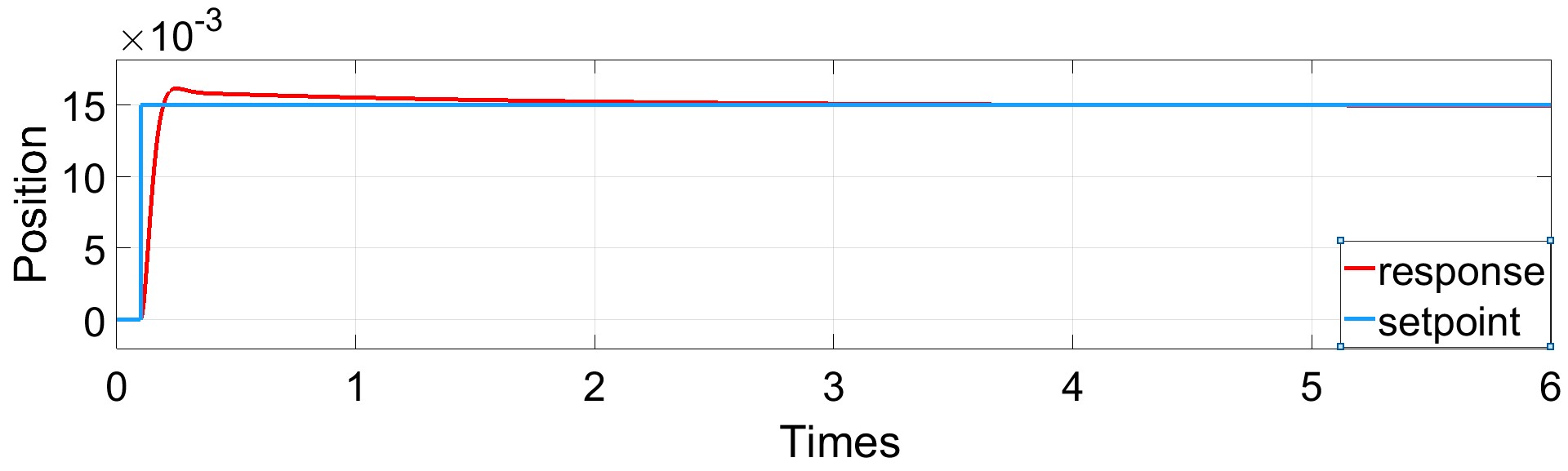
| This section presents numerical simulations of the Surgical Robot Manipulator and BELBIC controller to examine the performance of the proposed controller. Figure 7 shows the simulation result of the proposed controller applied to the model, where the figure shows the position of the robot manipulator end. |
|
| |
|
 |
|
| Figure 7 the simulation result of the proposed controller applied to the model. |
|
| |
|
| |
|
| the performances of the proposed controller were compared with a good tuned PID controller, that is tuned with Nikolas and Zegler. Figure 8 shows the simulation result of good tuned PID controller applied to the model. |
|
| |
|
 |
|
| Figure 8 The simulation result of the PID controller applied to the model. |
|
| |
|
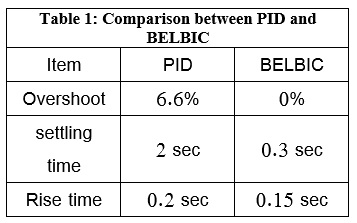
Comparison between the BELBIC controller and PID controller (table 1) shows that :
• In the PID controller, there is an overshoot, But in the BELBIC controller, there isn’t an overshoot.
• The setting time in the BELBIC controller is smaller than in the PID controller.
• The Rise time in the BELBIC controller is smaller than in the PID controller. |
|
| |
|
 |
|
| |
|
So BELBIC controller is better than the PID controller, in control Surgical Robot Manipulator.
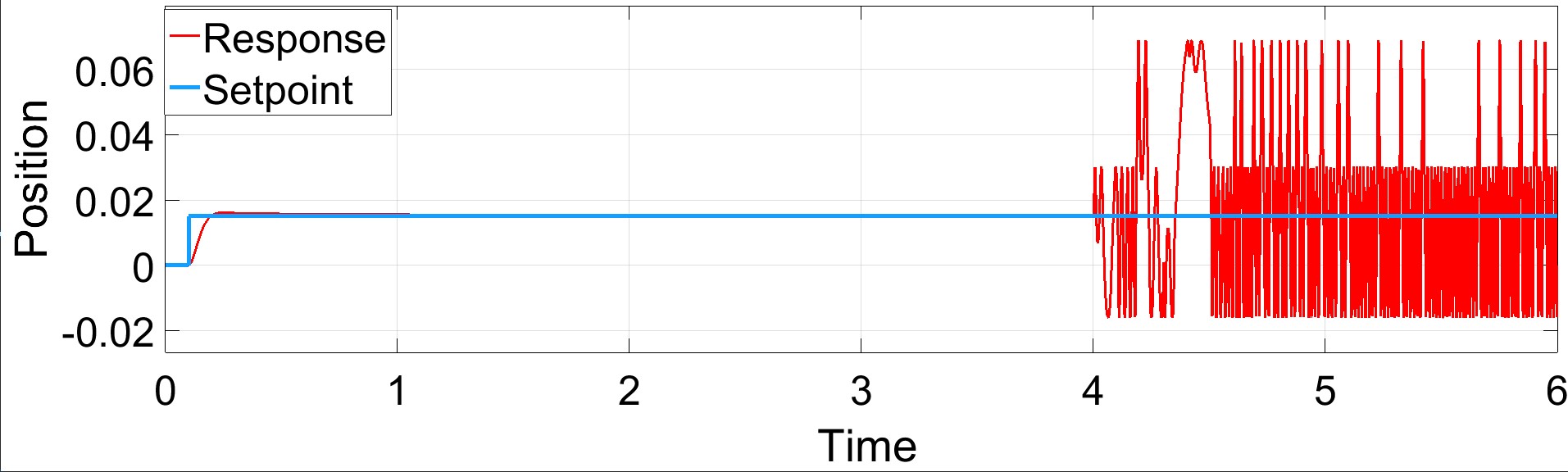
Let’s examine the system response under the control of PID and Proposed BELBIC when we have packet loss between the 4th and 5th seconds.
Figures 9 and 10 show the responses of the PID controller and the proposed controller respectively. |
|
| |
|
 |
|
| Figure 9: response of the controlled system with packet loss when PID is applied |
|
| |
|
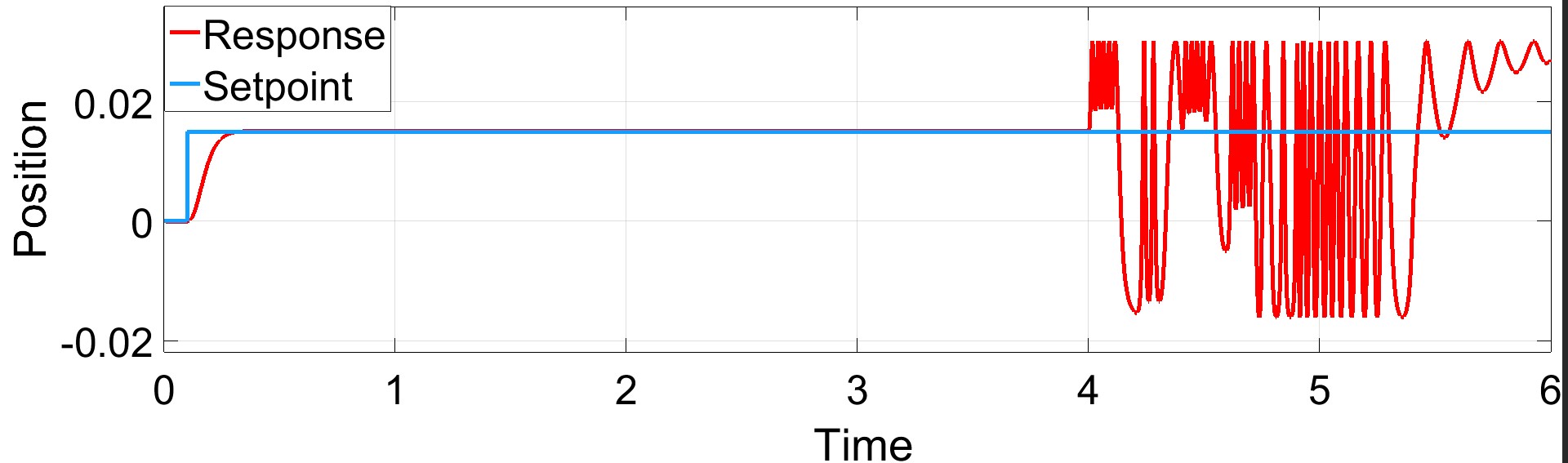 |
|
| Figure 10: response of the controlled system with packet loss when BELBIC is applied |
|
| |
|
| From this figure, we can see that the system is unstable and does not reach the goal point when both controllers are applied, so these controllers can’t overcome the packet loss problem. |
|
| |
|
| 6. Developed Structure of Proposed BELBIC |
|
| To improve the performance of BELBIC with packet loss, the structure of the BELBIC controller is improved by adding a memory block to the structure, as depicted in Figure 11. This memory block helps the controller to use the past information So the feedback signals didn’t return to zero when the packet loss has occurred. |
|
| |
|
 |
|
| Figure 11. Modified BELBIC structure |
|
| |
|
| the performance of the improved controller is reexamined under the same conditions mentioned earlier. Figure 12 shows the response of the improved controller applied to the model. The results show that the system with modified BELBIC overcomes the problem and the system is stable and reaches the goal point. |
|
| |
|
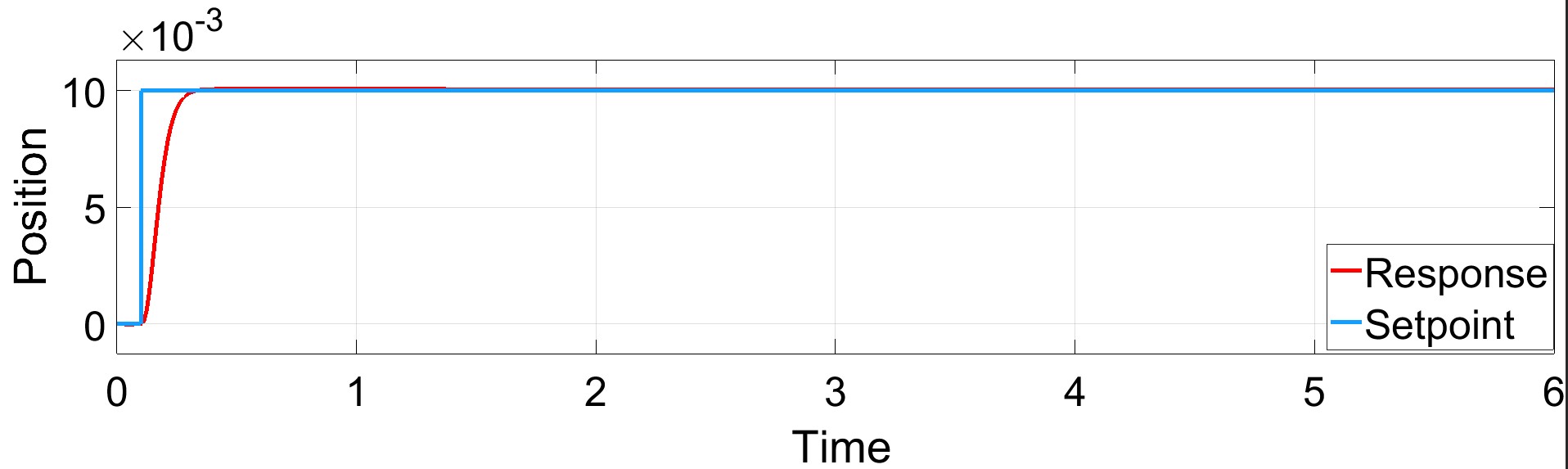 |
|
| Figure 12: response of the controlled system when the modified BELBIC is applied with packet loss |
|
| |
|
From this figure we can see that the system is stable and reach the goal point, so the controller can overcome the packet loss problem.
Now let’s check the system response under the control of modified BELBIC with packet loss between the 4th and 5th seconds. when we have a specific path that the Robot Manipulator has to follow. This response has been shown in Figure 13. |
|
| |
|
 |
|
| Figure 13: response of the controlled system when the modified BELBIC is applied with packet loss on a specific path |
|
| |
|
| As we can see in Figure 13, the system follows a specific path, and the controller can lead the robot manipulator to end on the path even if there is packet loss, and the system is stable and reaches the goal point. |
|
| |
|
| 7. Conclusion |
|
• In this paper the Brain Emotional Learning Based Intelligent Controller is used to control Surgical Robot Manipulator.
• The simulation result of controlling the Surgical Robot Manipulator with a proposed controller is compared to a well-tuned PID.
• The results show the satisfactory performance of applying BELBIC to the Surgical Robot Manipulator. and the BELBIC controller is better than the PID controller, in control Surgical Robot Manipulator.
• The simulation results show that the BELBIC controller can’t solve the packet loss problem. Therefore, a modified BELBIC structure is proposed and the system is examined with packet loss.
• The simulation results show that the modified BELBIC can overcome the packet loss problem.
• The simulation results show that the modified BELBIC can lead the system to follow a specific path in spite of the packet loss problem. |
|
| |
|
| References |
|
1. L. Sciavicco and B. Siciliano, (2000) "Modeling and Control of Robot Manipulators", 2nd ed. London, U.K., Springer-Verlag, pp. 14-17, 19-23, 26, 45, 49, 59, 60, 67, 99, 100.
2. Z. Bingul, (2012)"Serial and Parallel Robot Manipulators - Kinematics, Dynamics, Control and Optimization", InTech, 14, 15, 17, 19, 20, 22, 49, 59, 60, 66, 67.
3. T. R. Kurfess, (2005) "Robotics and automation handbook", CRC.
4. C. Wu, (1986) "Robot accuracy analysis based on kinematics", IEEE Journal of Robotics and Automation, vol. 2, no. 3, , pp. 171-179.
5. J. J. E. Slotine and W. Li, (1991) "Applied nonlinear control", Prentice hall Englewood Cliffs, NJ, vol. 461.
6. L. Cheng, Z. G. Hou, M. Tan, D. Liu and A. M. Zou, (2008) "Multi-agent based adaptive consensus control for multiple manipulators with kinematic uncertainties", IEEE international conference of intelligent control (ISIC), pp. 189-194.
7. B. Siciliano and O. Khatib, (2018) Springer handbook of robotics: Springer-Verlag New York Inc.
8. B. Armstrong, O. Khatib and J. Burdick, (2020), "The explicit dynamic model and inertial parameters of the PUMA 560 arm", IEEE International Conference on Robotica and Automation, pp. 510-518.
9. Ohri, J., Vyas, D. R., & Topno, P. N. (2011). Comparison of robustness of PID control and sliding mode control of robotic manipulator. International Symposium on Devices MEMS Intelligent Systems and Communication (ISDMISC), Bhopal, India, 5–10.
10. Getachew, D. (2018). Sliding mode control of a two degree of freedom robot arm using permanent magnet synchronous motor.
11. Alassar, A. Z., Abuhadrous, I. M., & Elaydi, H. A. (2010). Comparison between FLC and PID controller for 5DOF robot arm. 2nd IEEE International Conference on Advanced Computer Control, 5, 277–33. Shenyang, China.
12. Piltan, F., Yarmahmoudi, M. H., Shamsodini, M., Mazlomian, E., and Hosainpour, A. (2012a). PUMA-560 robot manipulator position computed torque control methods using Matlab/Simulink and their integration into graduate nonlinear control and Matlab courses. International Journal of Robotics and Automation, 3(3), 167–191.
13. Piltan, F., Rahmdel, S., Mehrara, S., and Bayat, R. (2012b). Sliding mode methodology vs. Computed torque methodology using matlab/simulink and their integration into graduate nonlinear control courses. International Journal of Engineering, 6(3), 142–177.
14. haei, S. E. (2010). Sliding mode control of robot manipulators via intelligent approaches.
15. Kapoor, N., & Ohri, J. (2013). Fuzzy sliding mode controller (FSMC) with global stabilization and saturation function for tracking control of a robotic manipulator. Journal of Control and Systems Engineering.
16. Anh, H. P. H., Kien, C. V., Son, N. N., & Nam, N. T. (2018). New approach of sliding mode control for nonlinear uncertain pneumatic artificial muscle manipulator enhanced with adaptive fuzzy estimator. International Journal of Advanced Robotic Systems, 1–11.
17. Zhang, H., Fang, H., Zhang, D., Luo, X., & Zou, Q. (2020). Adaptive fuzzy sliding mode control for a 3-DOF parallel manipulator with parameters uncertainties.
18. Caro Lucas, Daniel Shahmirzadi, (2004 )“Introducing Belbic: Brain Emotional Learning Based Intelligent Controller”, Intelligent Automation and Soft Computing
19. Zahra Beheshti, Zaiton Mohd, (2010)“A Review of Emotional Learning and Its Utilization in Control Engineering”, Int. J. Advance. Soft Comput. Appl. Vol. 2, No.2.
20. J. Moren, C. Balkenius, (2000), "A Computational Model of Emotional Learning in the Amygdala", Cybernetics and Systems, Vol. 32, No. 6, pp. 611- 636.
21. E. T. Rolls, (1995)A Theory of Emotion and Consciousness, and Its Application to Understanding the Neural Basis of Emotion. Cambridge, MA: MIT Press.
22. S. Maren, (1999), "Long-Term Potentiation in the Amygdala: A Mechanism for Emotional Learning and Memory", Trends in Neurosciences, Vol. 22, No. 12, pp. 561-567
23. J. Moren, C. Balkenius, (2000), "A Computational Model of Emotional Learning in the Amygdala", Cybernetics and Systems, Vol. 32, No. 6, pp. 611- 636
24. Mohammad Jafari, Hao Xu, Luis Rodolfo Garcia Carrillo, (2021) “A neurobiologically-inspired intelligent trajectory tracking control for unmanned aircraft systems with uncertain system dynamics and disturbance”, Transactions of the Institute of Measurement and Control.
25. Javad Abdi, Azam FamilKhalili, (2018) “Brain Emotional Learning Based Intelligent Controller via Temporal Difference Learning”, Proceedings of theInternational Conference on Mathematical Methods, Mathematical Models and Simulation. |
|
| |
|
| |
|
| |
|
|